四探针法是如何测出薄层电阻的呢？

使用四探针法测量方块电阻

方块电阻（又称表面电阻或表面电阻率）是表征导电和半导体材料薄膜的一种常见电学特性。它用于衡量通过材料薄方块的横向电阻，即方块相对两边之间的电阻。方块电阻相较于其他电阻测量的关键优势在于，它与方块的尺寸无关，这使得不同样品之间的比较变得简单。

方块电阻可通过四探针轻松测量，且在高效钙钛矿光电器件的制备中至关重要，这类器件需要低方块电阻材料来提取电荷。

一、方块电阻的应用

方块电阻对于任何旨在让电荷沿其表面（而非穿过）传输的材料薄膜而言，都是一项关键特性。例如，薄膜器件（如钙钛矿太阳能电池或有机发光二极管）需要导电电极，这些电极的厚度通常在纳米到微米范围内。电荷在发光二极管器件内的移动过程中，电极必须横向传输电荷，且需要低方块电阻以减少传输过程中的损耗。当试图扩大这些器件的尺寸时，这一点变得更为重要，因为电荷在被提取前需要在电极中传输更远的距离。

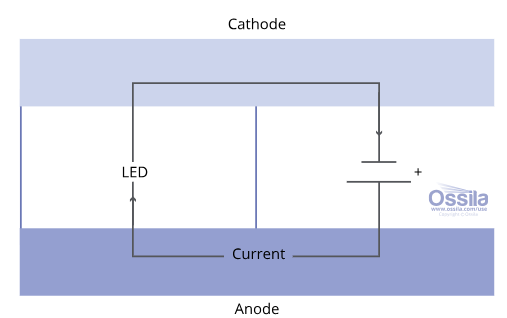
显示电流通过电极横向流向活性材料。电极的方块电阻会影响到达发光二极管的电流大小，进而影响其性能。

此外，若已知方块电阻和材料厚度，还可计算出电阻率和电导率。这使得仅通过方块电阻测量就能对材料进行电学表征。

二、四探针法测量方块电阻

（一）基本原理

测量方块电阻的主要技术是四探针法（又称开尔文技术），该方法通过四探针仪实现。四探针仪由四个等间距、共线的电探针组成。

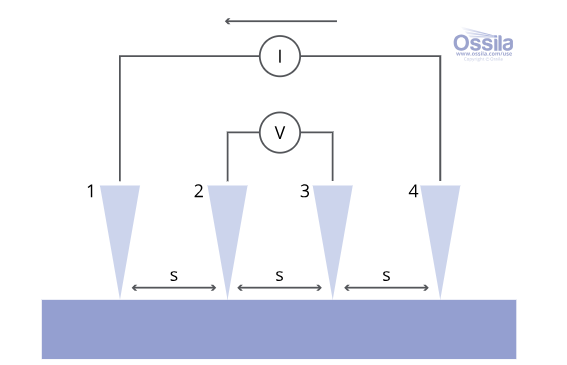
四个探针间距相等（s），与表面接触。电流（I）通过探针1注入，通过探针4收集，同时在探针2和3之间测量电压。

其工作原理是在外侧两个探针之间施加直流电流（I），并测量内侧两个探针之间产生的电压降。

（二）方块电阻公式

方块电阻可通过以下公式计算：

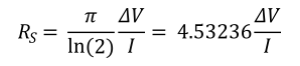
其中，Rs 方块电阻，ΔV 为内侧探针之间测量的电压变化，I为外侧探针之间施加的电流。方块电阻的测量单位通常为Ω/□（欧姆/方块），以区别于体电阻。

需要注意的是，该公式仅在以下条件下有效：

1. 被测材料的厚度不超过探针间距的40%

2. 样品的横向尺寸足够大

若不满足上述条件，则需要引入几何校正因子，以考虑样品的尺寸、形状和厚度的影响。校正因子的值取决于所使用的几何结构。

若已知被测材料的厚度，可利用方块电阻计算其电阻率：

其中， ρ 为电阻率， t 为材料厚度。

（三）消除接触电阻

使用四探针法进行电学表征的主要优势之一是能够消除测量中的接触电阻和导线电阻。

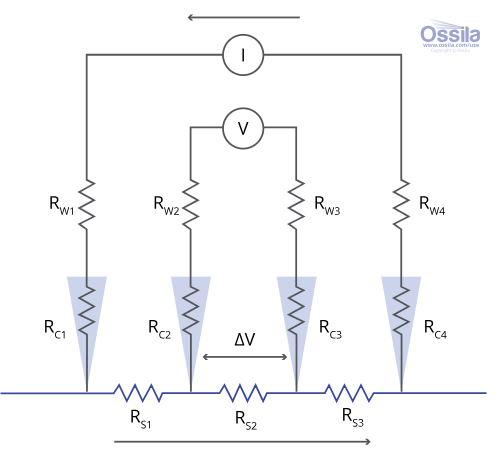
显示导线电阻 (RW)、接触电阻(RC)和样品电阻(RS)。箭头表示电流流向。

施加的电流I通过外侧探针进出样品，并在样品中流动。电压表通常具有高阻抗，以避免影响被测电路，因此内侧两个探针中无电流流过。仅测量内侧探针之间的电压，这意味着导线电阻（RW2 和 RW3）和接触电阻（RC2 和RC3）不会对测量产生影响。因此，测量到的电压降（ΔV）由样品电阻（RS2）引起。这简化了方块电阻公式，只需ΔV和施加的电流即可计算出 RS2（即方块电阻）。

三、几何校正因子

上述方块电阻公式与样品几何形状无关，但这仅适用于样品尺寸显著大于探针间距（通常尺寸为探针间距的40倍以上），且样品厚度小于探针间距40%的情况。若不满足这些条件，探针之间可能的电流路径会因靠近样品边缘而受到限制，导致方块电阻被高估。为解决这一问题，需要基于样品几何结构引入校正因子。

（一）圆形样品

对于直径为d的圆形样品，在样品中心测量时，校正因子可通过以下公式计算：

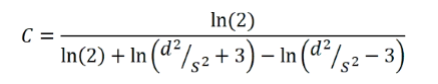
其中， s为探针间距。当d >> s 时，该公式的值趋近于1，此时可使用未校正的公式。

（二）矩形样品

对于矩形样品，几何校正因子的确定稍复杂，没有现成公式，需使用经验确定的校正因子表。该表中的值仅适用于探针在样品中心接触，且与样品最长边（l）平行对齐的情况。

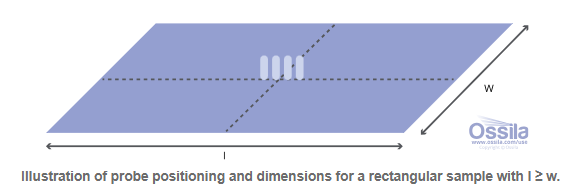
l ≥ w

例如，假设上图中的矩形样品长边l=20mm，短边w=10mm，所使用探针的间距S=2mm。此时，l/w=2，w/s=5，在表中查找满足这两个值的校正因子，即l/w=2列和w/s=5行对应的校正因子C=0.7887。将测量得到的方块电阻乘以该值，即可得到样品的正确方块电阻。

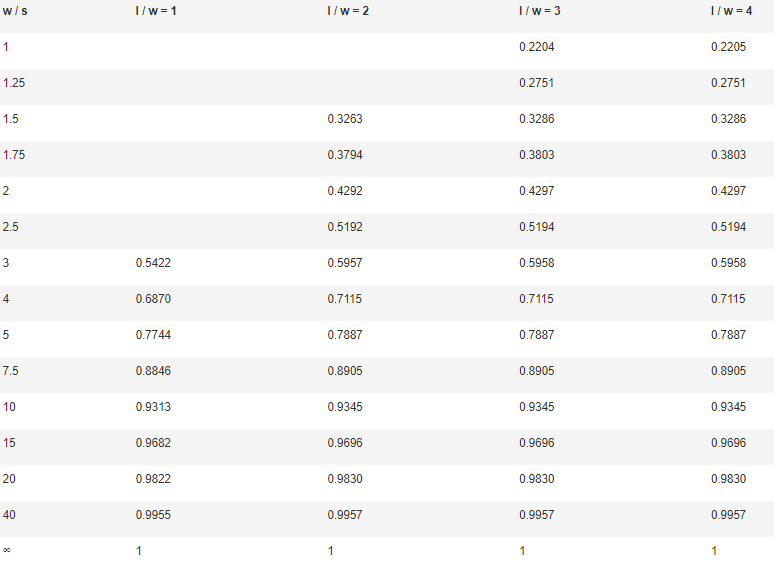
并非所有样品都能符合这些类别。若遇到这种情况，建议使用三次样条插值法估算样品的合适校正因子。

需要注意的是，上述圆形和矩形样品的校正因子仅适用于在样品中心进行的测量。若测量不在中心位置，则需要使用不同的校正因子。

（三）其他形状和探针位置

对于不同形状的样品以及非中心位置的测量，需要使用其他校正因子。

若样品形状不规则，可考虑其更接近矩形还是圆形，然后估算该形状能容纳的样品尺寸。

（四）厚样品

若被测样品的厚度大于探针间距的40%，则需要额外的校正因子。所使用的校正因子取决于样品厚度（t）与探针间距（s）的比值，部分可能的值如下表所示：

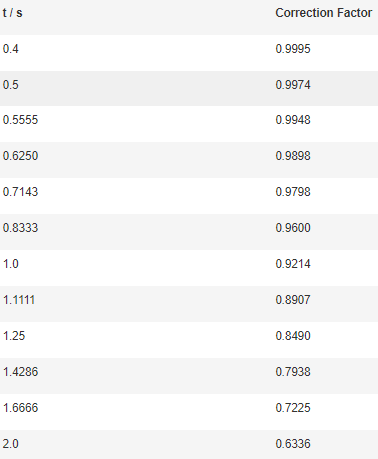
与矩形样品一样，若t/s不等于表中给出的值，建议使用三次样条插值法估算样品的合适校正因子。

四、探针公式推导

为确定如何使用四探针测量薄膜的方块电阻，需先评估一个简化场景。假设有一个极尖的探针与导电材料的半无限体积（除朝向探针的方向外，所有方向均无限延伸）接触并注入电流（通过施加电压）。

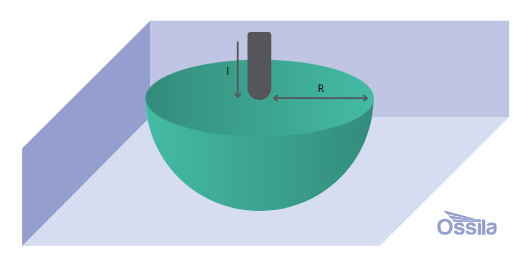
绿色半球是半径为r的注入电流壳层

电流从接触点向外流过同心半球形等势壳层，每个壳层的电流密度（J）为：

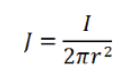
其中，r为到探针的径向距离（2πr2 为半球的表面积）。应用欧姆定律（E = ρJ），其中每个壳层的电场等于壳层厚度上的电压降，即-ΔV / Δr （该术语为负，因为电压随r增大而减小），且壳层厚度趋近于零，得到以下方程：

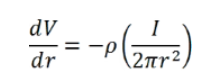
对r到r'积分可得：

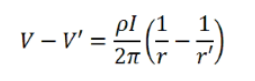
应用当r趋近于无穷大时V趋近于零的边界条件，方程简化为：

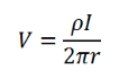
现在假设有四个极尖的探针（标记为1至4）与半无限导电材料接触，它们共线且间距相等（s）。设置为通过探针1注入电流，由探针4收集电流。若假设每个探针具有等效边界条件，则任意点的电压等于每个探针单独产生的电压之和，即：

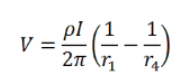
其中，r1和r4分别是到探针1和探针4的径向距离。在探针2和3之间测量电压。使用上述方程，探针2和3处的电压分别为：

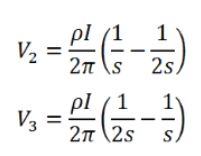
因此，探针2和3之间的电压变化（ΔV）为：

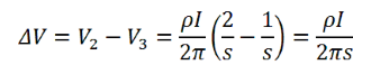
因此，探针之间的电阻率为：

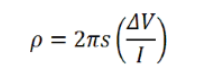
该表达式仅适用于半无限体积的情况，不适用于薄膜。但可通过类似分析推导新的表达式。同样，假设有一个极尖的探针与厚度为t的材料薄膜接触并注入电流。

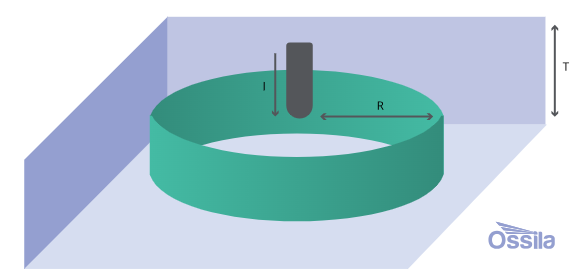
绿色圆柱是半径为r的注入电流壳层

在这种情况下，电流从探针（通过材料）流过短圆柱形等势壳层，每个壳层的电流密度为：

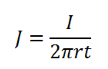
应用与之前相同的电场条件（欧姆定律和壳层厚度趋近于零），每个壳层的电场为：

已知电阻率定义为方块电阻乘以材料厚度，因此可代入上式得到：

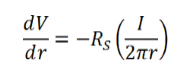
对r和r'积分可得：

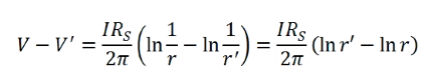
与之前不同，不能假设当r趋近于无穷大时电压趋近于零，因为无穷大的自然对数不为零。但这并不影响分析，因为四探针测量的是不同点之间的电压差(ΔV) 。

现在考虑与薄膜接触的四探针系统，附加条件是薄膜厚度（t）远小于探针间距（s）。对于由探针1注入电流并由探针4收集电流的情况，方程变为：

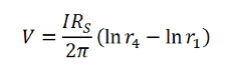
在探针2和3处测量的电压因此为：

因此，电压变化为：

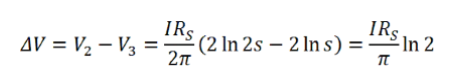
整理可得：

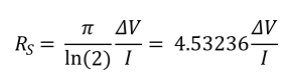
因此，通过测量内侧探针之间的电压变化和外侧探针之间施加的电流，可测量样品的方块电阻。

五、       快速准确的方块电阻测量

Ossila四探针仪使薄膜的方块电阻、电阻率和电导率测量变得快速简便。

- 可在100mΩ/□至10MΩ/□的广泛范围内测量方块电阻，实现对各种材料的精确表征。

- 通过平衡正负电流以消除电压偏移来计算平均方块电阻，显著提高测量精度。

- 可表征直径达6英寸（152.4mm）的大样品。大样品对校正因子的依赖性更小，测量更准确。

- 通过PC使用免费且直观的Ossila方块电阻精简软件实现无缝控制。

- 为增加多功能性，可选择Plus型号，其内置软件和显示屏，无需PC即可表征样品。